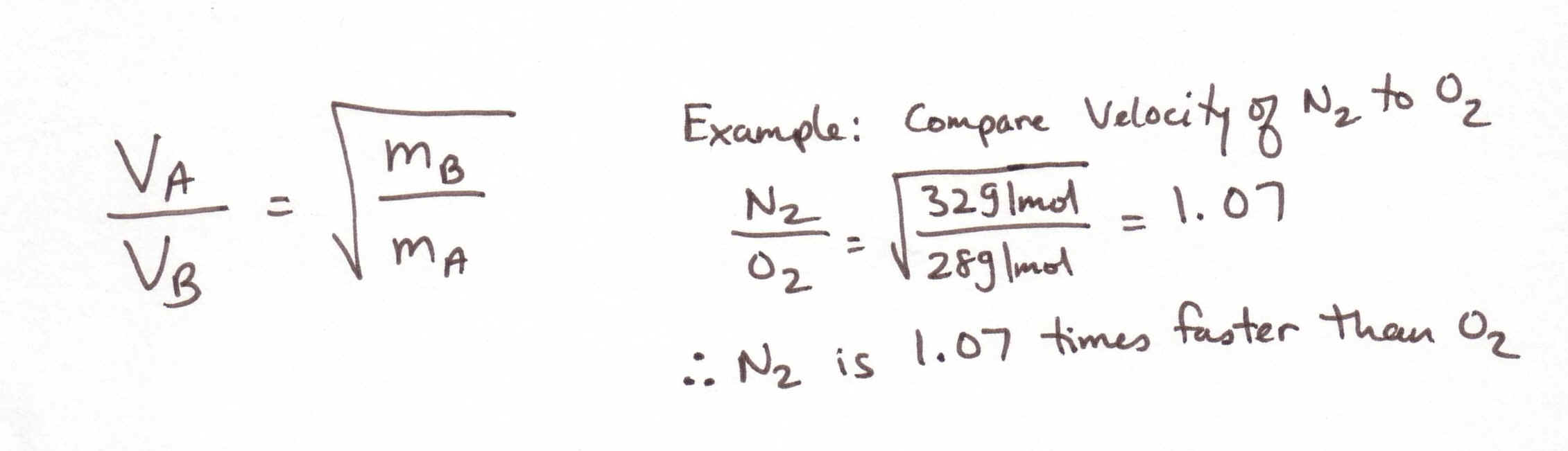Chapter 11 Notes –
Molecular Compositions of Gases
1.
The ideal gas law PV=nRT. (page 342) Can also be written: PV
= (mass/molar mass) RT
P= pressure, V= volume, n = number of moles of gas, R = universal gas constant,
T = Temperature.
How did they arrive at the value for R? There are 2 possible values for R:
R= PV/nT
We assume that R is at STP which is 0oC (or 273K) and 101.325kPa. Volume of 1 mole of gas at STP is 22.4L
Value #1: R= (101.325kPa) (22.4L)/(1mole) (273K) = 8.315 kPa L/mole K
Value #2:
R= (1 atm) (22.4L)/(1 mole) (273K) = 0.0821
atm L/mole K
How to do problems
with PV=nRT:
- You must always remember to be sure that you have the correct units in order to do a problem. Remember that pressure can be measured in atm or kPa. Volume should always be in Liters (which is the same as dm3). The n is always in units of moles and the Temperature is always measured in units of Kelvin. If the pressure is in atm, use an R value of 0.0821. If the pressure is in kPa, use an R value of 8.315.
- If you get a problem with the number of grams of a substance,
use the periodic table to convert grams into moles before doing the problem.
REMEMBER YOUR DIATOMIC ATOMS!
2. The Combined gas law of Charles’ and Boyles:
It is not always the case that temperature will remain constant (Boyle’s law) or that pressure will remain constant (Charles’ law). Sometimes, pressure, volume and temperature all change. Therefore, you can combine Charles’ and Boyle’s law to read:
P1V1T2 = P2V2T1.
How to do combined gas law problems:
-So long as the P1 and P2 are in the same units and the V1 and the V2 are in the same units, do not worry about converting these. If P1 is in atm and P2 is in kPa, then you will have to change one into the other. If V1 is in mL and V2 is in L, then you will have to change one into the other.
- Your temperature units
will always need to be converted into Kelvins.
3. The ideal gas law meets stoichiometry: (p. 347-350)
So
far, we have used stoichiometry to figure out how many grams of a substance can
be made from so many grams of another substance.
Now, we are going to use it to find out how many Liters of a substance
can be created from grams of a substance.
How to do gas law stoichiometry problems:
-You must know the temperature and pressure of the reaction
-You must first balance the chemical equation (just like regular stoichiometry)
Example: How
many liters of hydrogen gas will be liberated upon the decomposition reaction of
10.0 grams of water at STP.
1. Balance the equation: 2H2O ---à 2H2 + O2.
2. Do the stoichiometery.

3. Use the moles of H2 created to do an ideal gas law problem where you solve for volume. Since it is at STP, the pressure is 1 atm (or you could use 101.325 kPa – your choice) and 273K.
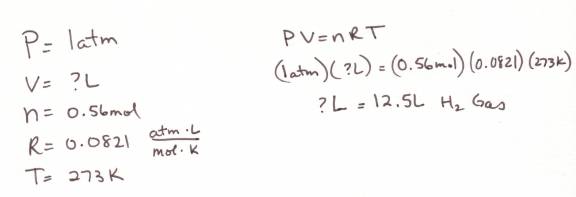
4. Gas Stoichiometry and Limiting Reagents: (Not very well described in the textbook)
If
you are given 2 volumes of reactants, then you have to determine which one is
your limiting reagent. For example:
4.0 L of methane (CH4) and 0.50 L of Oxygen are reacted
together to produce carbon dioxide and water.
Which is the limiting reagent?
First, write a balanced equation: CH4 + 2O2 ------à CO2 + H2O
Second, do as you would normally do with a limiting reagent problem, go “into” methane and come out Oxygen.

You can see that you would need to have 8.0 L of oxygen to
complete this reaction. Therefore,
Oxygen is your limiting reagent. You
can assume Liters to be the same as moles in determining limiting reagents
because all gases have the same number of moles in them at the same temperature,
pressure and volume. THIS ONLY WORKS FOR GAS-GAS OR GAS-MASS STOICHIOMETRY
PROBLEMS.
5.
Density and Gas Laws: (p.
345)
As the pressure, volume and temperature of a gas change, so does the gas’ density:
As Pressure on a gas increases, the density of that gas increases.
As the volume of a container containing a gas increases, the gas density decreases
As the temperature on a gas increases,
the density of the gas decreases.
Doing problems with Density and gas laws:
All temps should be in Kelvin. Pressure
and Volume don’t matter so long as their 1 and 2 values are in the same units.
If one or more of the following values remains constant, then its value
is “1” in the equation and thus you can ignore it. Example: If the
temperature remains constant, then T1/T2 = 1.
Old gas density (in g/mL) x (P2/P1)
x (V1/V2) x (T1/T2) = new gas
density (in g/mL)
6. Kinetic Molecular Theory: (p. 303-304 of chapter 10)
Be sure to read the 5 basic points about the Kinetic Molecular Theory
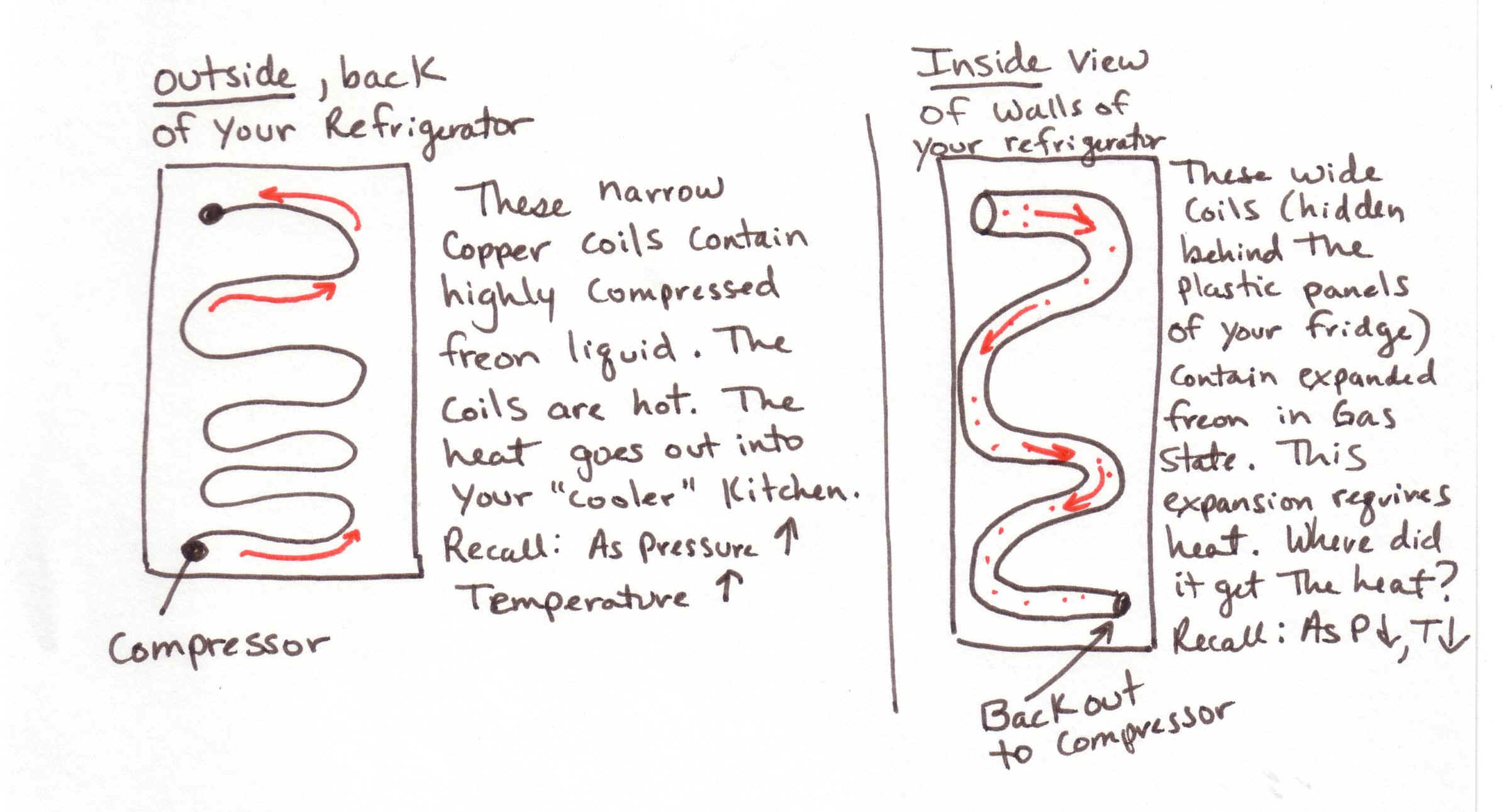
You also need to know that if temperature of a gas increases so does its pressure.
Likewise,
if pressure decreases rapidly, so does temperature. This is how your refrigerator works. By reducing the pressure of the gas (freon) very quickly, the
temperature is lowered very quickly. You
have a compressor in your refrigerator to press the freon back together again
and then it is released over and over….(SEE DRAWING BELOW)
7.
Grahm’s Law of diffusion: (p. 351-355)
Simply
put, lighter gas molecules travel faster than slower ones.
Grahm’s
law is used to determine the relative speed at which two molecules will travel
in relation to one another. See his
equation below where v = velocity and m = mass of the molecule.
The lighter molecule should be labeled A and the heavier one B.
Bottom line: The
kinetic energy of two gas molecules at the same temperature is the same.
But, the Velocity of two gas molecules at the same temperature depends
upon their mass. Lighter
molecules will have a faster velocity.
How to do Grahm’s law problems: Turn to page 352 and do the example on p. 355. See example below: