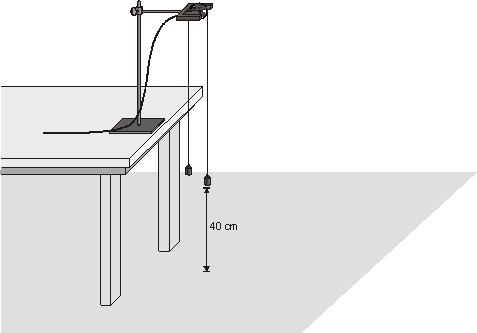
Atwood’s Machine

A classic experiment in physics is the Atwood’s machine: Two masses on either side of a pulley connected by a light string. When released, the heavier mass will accelerate downward while the lighter one accelerates upward at the same rate. The acceleration depends on the difference in the two masses as well as the total mass.

In this lab, you will determine the relationship between the two factors which influence the acceleration of an Atwood’s machine using a Photogate for measuring acceleration.

Figure 1

objectives

·   Use a Photogate to study the acceleration of an Atwood’s machine

·   Determine the relationships between the masses on an Atwood’s machine and the acceleration.

Materials

PRE-LAB questions:  You do not need to copy the questions.

1.   If two equal masses are suspended from either end of a string passing over a light pulley (an Atwood’s machine), what kind of motion do you expect to occur? Why?

2.  What would happen if you gave one of those equal masses a short "tug".  Would they both accelerate or move with a constant velocity?  Why did you choose the answer that you did?  This answer involves one of Newton's three basic laws of motion.

3.  What would the graph of a velocity vs. time look like for the short "tug" you gave the masses in question #2?  Would it have a positive slope, a negative slope or a slope of zero? (draw the graph too).  HINT:  Think about what happens when you give them the "tug"  what speed will they reach?

4.  What does the slope of a velocity vs. time graph tell you?

5.   For  an Atwood’s machine, how would you expect the acceleration to change if you:

      (Answers should be qualitative - no numbers.  Assume you put these masses on, hold the system still and then let it go)

a.    Move mass from one side to the other, keeping the total mass constant?  (in other words, you have a total of 20 grams to start with.  Say you put 15 grams on one side and 5 on the other....  Then you put 17 grams on one side and 3 grams on the other...... what would happen?)

b.    Gradually increase the mass of both sides?  (in other words, you have 20 grams on each side.  You add a 5 gram mass to each side so that each side is now 25 grams.... what would happen?)

6.   Why do the two masses have the same acceleration_net? (Read example 4.6 p. 114-115 if you need some help on this one).  This is a simple explanation and has to do with one of Newton's three basic laws (not the same law you used in pre-lab question #2).

7.   Draw a free-body diagram of the left side mass (m₁ – the greater mass). Draw another of the right side mass (m₂ – the lesser mass). Include all forces acting on each mass.

8.  Write an equation that sets the forces acting on m₁ equal to the overall a_net on m₁.  Hint:  it will involve tension.

9.  Write an equation that sets the forces acting on m₂ equal to the overall a_net on m₂.  Hint:  it will involve tension.

Procedure:

Part I  Keeping Total Mass Constant

For this part of the experiment you will keep the total mass used constant, but move weights from one side to the other. The difference in masses changes.

1.   Set up the Atwood’s machine apparatus as shown in Figure 1. Be sure the heavier mass can move at least 40 cm before striking the floor.

2.   Connect the Photogate with Super Pulley to DIG/SONIC 1 of the LabPro or DG 1 of the Universal Lab Interface.

3.   Open the file in the Experiment 10 folder of Physics with Computers. A graph of velocity vs. time will be displayed.  Make sure that the scale of the x-axis is set for AUTOSCALE with a minimum of 0 seconds and a maximum of 7 seconds.  Make sure that the scale of the y-axis is set for MANUAL SCALE –0.1 to 0.5.  If you mess up, you can either correct the scales by double-clicking on one of the numbers on the axis OR, just close out Logger-Pro and re-open it since it is set for this in its default parameters.

4.   Arrange a collection of masses totaling 100 g on m2 and a 100-g mass on m1.  

     a.  Hold them steady and then let them go.  What is their acceleration?  What is their velocity? This one is easy.  Do you think it will accelerate at all if the masses are equal on both sides?  

         Write your answer here:  Acceleration:   ____________________.   

                                                    Velocity ______________________

     b.  Give one of the masses a short "tug".  What is their acceleration?  What is their velocity?  What is the slope of the line?

    Write your answer here:  Acceleration:   ____________________.   

                                              Velocity ______________________

                                              Slope of the line  _________________

5.   Arrange the masses so that you have 110 g on one side (m₁) and 100 g on the other (m₂). Look at the Data Table for Part I:  Keeping Total Mass Constant at trial #1 (I have entered some things for you in red.  You need to complete any blanks in the data tables)

6.   Position m1 as high up as it can go. Click  to begin data collection. Steady the masses so they are not swinging. COUNT TO THREE MISSISSIPPI BEFORE RELEASING MASSES – THE PHOTOGATE TAKES A FEW SECONDS TO START WORKING. Catch the falling mass before it strikes the floor or the other mass strikes the pulley.

7.   Click the Examine button  (Or go up to the pull-down menu bar “Analyze”, the “examine” feature is right there) and select the region of the graph where the velocity was increasing at a steady rate. Click the Linear Regression button   (Or choose linear fit under “Analyze”)to fit the line y = mx + b to the data. Record the slope, which is the acceleration, in the data table.  Realize that the slope of a velocity vs. time graph is acceleration (sounds like a great general question to me!)

8.   Continue to move masses from m₂ to m₁ in 10-g increments, changing the difference between the masses, but keeping the total constant (see the data table  for Part I below if you are confused). Repeat Steps 6 - 7 for each mass combination. Repeat this step until you get at least five different combinations.

Part II  Keeping The Mass Difference Constant

For this part of the experiment you will keep the difference in mass between the two sides of the Atwood’s machine constant and increase the total mass.

9.   Put 120 g on m1 and 100 g on m2.

10.   Repeat Steps 6 – 7 to collect data and determine the acceleration.

11.   Add mass in 20-g increments to both sides, keeping a constant difference of 20 grams. Record the resulting mass for each combination in the data table. Repeat Steps 6 - 7 for each combination. Repeat the procedure until you get at least five different combinations.

Data Table

CALCULATIONS/Analysis:

1.   Using Graphical Analysis, plot a graph of acceleration vs. Dm, using the Part I data. Based on your analysis of the graph, what is the relationship between the mass difference and the acceleration of an Atwood’s machine?  (Do a curve fit of this line and leave it on your graph.  It should be linear)

Answer the question "what is the relationship between the mass difference...." here:  Put your data table/graph here too.

2.   Using Graphical Analysis, plot a graph of acceleration vs. total mass, using the Part II data. Based on your analysis of the graph, what is the relationship between total mass and the acceleration of an Atwood’s machine?  (Do a curve fit of this line and leave it on your graph.  It should be Quadratic – a parabola)

      Answer the question "what is the relationship between total mass and acc....." here:  Put your data table/graph here too.

QUESTIONS:

1.   Find an expression for the acceleration of m1 in terms of m1, m2, and g.   (Hint:  F_net = m₁g – m₂g.  Use that formula and the sum of m₁ and m₂ to solve for acceleration.  Remember that the acceleration is the same for m₁ and m₂)

2.   For each of the experimental runs you made, calculate the expected acceleration using the formula you determined in the previous question.  Find the % error between your expected accelerations and the actual ones you got on the data table. Are the experimental acceleration values low or high? Why?

3.   Create an equation for finding the mass of m₁ if you know the following:  m₂ and a (acceleration is determined by dropping the masses and finding the slope of the resulting velocity vs. time line)  (Hint:  Algebraically re-arrange the formula you found in question #1 and set it equal to m1.  Test it out with some data to see if it works.  Don’t be surprised if there is a negative value in the formula you come up with)

 What is due for this lab?:  Please put it in this order too!  You can just fill in the blanks along the way.  Just make sure you put your answers in red so that I can see them quickly.

1.  25 points for neatness/organization/following directions/completeness

2.  Pre-lab questions  25 points

3.  Data Table/Calculations  25 points (for both data table and GA and Calculations)

4.  Questions  25 points

How to submit this lab to me via-e-mail and SAVE A TREE!

1.  EDIT-SELECT ALL.  Then EDIT-COPY.  Then open MS Word and EDIT-PASTE this whole thing into a Word document.  Or, if you are using a Mac, you will have to copy it into some kind of HTML editor.  OR save it as an HTML file to your computer.

2.  Please put all answers to questions and data tables in RED font color!  That way, I can find your answers quickly.  You may answer right after the questions in the lab.  (example:  What do you think will happen if you put equal masses on both sides of the Atwood's machine?  We think that the machine will stay the same because...blah, blah, blah....)

3.  Put the names of each of your group members at the upper right hand corner of the very first page of the document.  Bold type the person who did the typing/major preparation for the lab.

4.  If you don't want to spend your entire life putting calculations into the computer, you can give me a "calculations" sheet which is written by hand on the date the lab is due.  I'll include it when I grade your lab.  For this lab, however, I think you can type all of your calculations since there really isn't that much "mathematical" calculations you need to do.  Most of it is done in your GA spreadsheet.

5.  How to name your MS Word File:  Use the initials of the person sending the document and then the name "atwood".  For example.  If I were sending the file, I would call it:  "gyatwood".  This way I won't end up with a bunch of files all called "atwood".  When I get your file, I will save it to my computer.  This is why I must have you title your file correctly - otherwise, your "atwood" file will overwrite some other students' "atwood" file.

6.  Send it to my e-mail address:  gyyoung@capousd.org  

IB students - this is an IB lab.  You will have one extra week to turn it in.